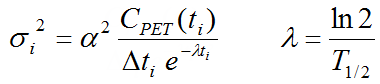PKIN Data Processing > Configuration and Fitting of Kinetic Tissue Models > Kinetic Model Fitting

Weighting is used to increase or decrease the influence of certain data samples on the fitting. For instance, initial samples with short acquisition duration and little uptake may be considered less reliable than the samples with longer durations in the presence of high uptake. The weights are multiplied with the squared residuals when calculating the Chi squares criterion.

In PKIN, several different weight definitions are supported. They can be specified on the Weighting pane using the list selection with the three entries Constant weighting, Prescribed weighting and Calculated weighting. The contents of the different selections are illustrated in parallel below.

Weights Specifications

Note that the weights are calculated from the definition of a standard deviation σi or the variance σi2 by
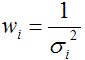
picture_2375

Constant
weighting

With constant weighting the same weight is applied to all residuals. Its size can be adjusted by the Scale factor and the radio button setting. In the case of TAC meanσi is obtained as the average of all values in the TAC multiplied by the Scale factor. Similarly, with TAC maxσi is obtained as the maximal TAC value multiplied by the Scale value. With All weights = 1 the weights are all set equal to 1 independent of the Scale (σi = σi2 = wi = 1). The scale factor doesn't have an impact on the fit result. It is only relevant when the wheiting definition is used for specifying the noise generated for Monte Carlo simulations.

Prescribed
weighting

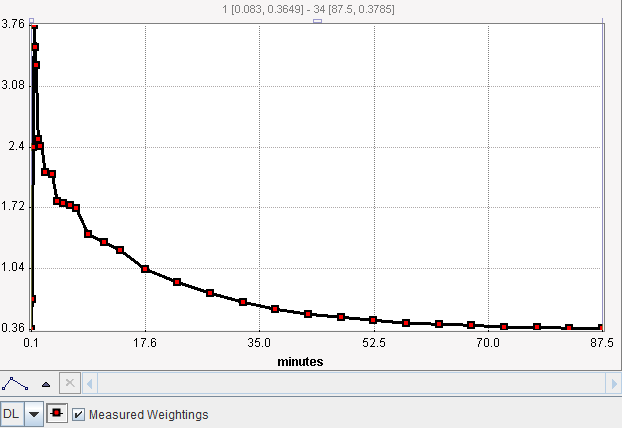
The default behavior of this method is to use the standard deviation of the pixel values in the VOI for calculating the TAC for weighting. This information is automatically available if the TACs have been transferred from the PMOD viewing tool to PKIN, and can be visualized using the button Show measured stdv as illustrated below.
picture_4883

This definition can be overwritten by user-defined weights which are to be loaded with the Load stdv from file button. Please see below how the file has to be formatted.

Calculated
weighting

With this selection the variance is calculated for each TAC value from an equation which may take into account the measured uptake, the radioactive decay, and the duration of the acquisition. The full equation is as follows:
picture_4884
It includes a Scale factor α, the decay-corrected Uptake CPET(ti) at frame mid-time ti, the frame Duration Δti, and the Decay constant λ which is obtained from the half-life T1/2 of the isotope. If the half-life has not yet been defined, it can be set on the SUV panel with the Edit Patient facility.
The settings of the radio buttons have the following effect on the equation above for calculating σi2:

▪Uptake:
Not considered: CPET(ti) is replaced by 1.
Measured value: CPET(ti) is used, corresponding to Poisson weighting. The effect is that more emphasis is given on low-uptake values than on high-uptake values. This may be helpful for example if the fit seems to not account enough for the tail of a decreasing function such as the input curve.
Measured value squared: CPET(ti) is replaced by CPET2(ti), corresponding to Relative weighting. With this option the influence of the uptake is further increased. It should be used with care because by squaring small (initial) uptake values (<<1) very small variances are generated which transform into heavy weighting. As a consequence, a few small uptake values may have excessive impact on the fit.

▪Duration:
Not considered: Δti is replaced by 1.
Measured value: The individual frame durations Δti are used, so that longer acquisitions are considered more reliable.

▪Decay:
Not considered: picture_4885 is replaced by 1.
Frame mid-time: is used, so that earlier acquisitions are considered more reliable.

Note: As a corrective measure, very small standard deviations of the first 1/3 data points (likely to have low uptake) are adapted to provide reasonable weights as follows: If the stdv is smaller than the average stdv and smaller than 50% of its successor, it is replaced by the stdv of the successor.

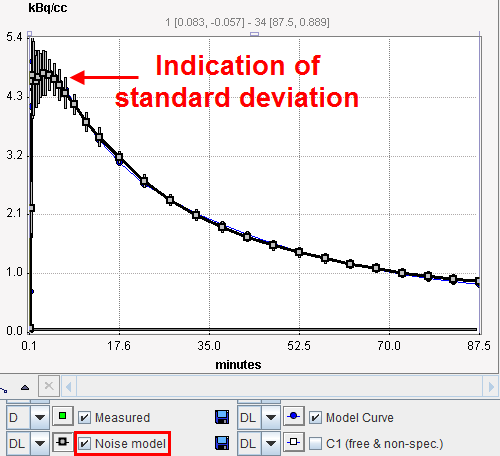
Whenever the configuration is changed, the standard deviation σi is calculated and plotted as an error bar around the measurements. This gives the user a visual feedback as a help in judging the adequacy of the specified weighting.

Measured Standard Deviation

Loading Externally Defined Weights

Some users might want to implement their own residual weighting schemes. To this end they should calculate the standard deviations σi for the different acquisition frames from which the weights will be calculated according to

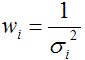
picture_2375

The σi should be prepared in a tab-delimited text file of the following form:

t[seconds]	standard-dev[kBq/cc]
10	0.10300076
30	0.01717448
50	0.01195735
70	0.01010257
etc	...

The header line is required. The first column represents the frame mid-times (although the values are not interpreted), and the second column the standard deviations in appropriate units. The number of entries must be equal to the number of acquisitions, and the columns separated by spaces or tabs. For example, such a file can be prepared in MS Excel and then saved as a text file with tab delineation.

This definition can be loaded by the Load stdv from file button available with Prescribed weighting.

Display of the Residuals

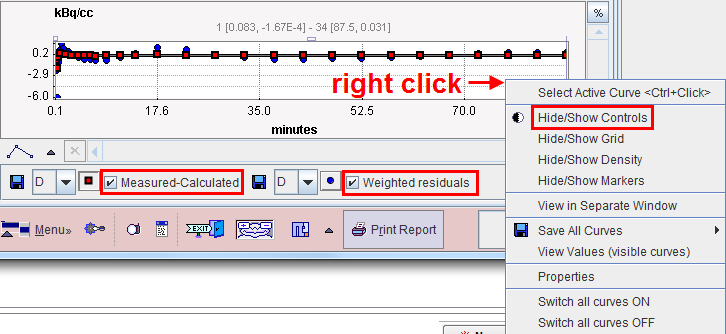
The curve area with the residuals per default shows the weighted residuals, that is the difference between the measurement and the model curve divided by the standard deviation.

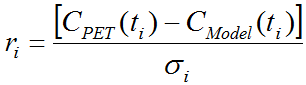
picture_8858

However, the raw residuals can also available. The context menu as illustrated below (right mouse click into the curve area) can be employed for showing/hiding the curve controls, which allow changing the displayed information.

picture_4886

Use of the Weights in Monte Carlo Simulations

Monte Carlo simulations require the generation of noise which is defined by a distribution type as well as its deviation characteristics. Assuming that the weights specification corresponds to the standard deviation of the measurement noise, the regional weighting specification is used in the Monte Carlo noise generation together with the distribution type. Note that the Scale factor has no impact on fitting, but that it is highly relevant in Monte Carlo simulations.

Residual Weighting

Residual Weighting