Least Squares Optimization
The fitting methods available optimize the agreement between the measurements and the model curve. Effectively, they minimize the difference between them, whereby the difference is described by the Chi Squares criterion (cost function) below:
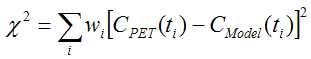
This expression implies that the squared residuals (measured value minus estimated model value) are multiplied by weights. To satisfy the requirements of least squares fitting, the weights wi should be related to the variance σi2 of the measurements by
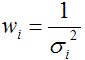
In this case, and provided that the distributions of the measurement error are normal, the estimate obtained is the maximum likelihood estimate. Under the same premise it is also possible to obtain standard errors of the model parameters as the square root of the diagonal elements in the covariance matrix.
Weighting of PET Data
The variance of reconstructed PET data is dependent on many factors, including the duration of the acquisition, the time since the scan start which needs to be compensated by a decay correction, scatter and random correction, the sampling volume, the reconstruction method, etc. Therefore, PET variance models used in weighting of the residuals during fitting are always approximations.
In his presentation Parameter Estimation: Least squares and why it gives you fits (Handouts of Pharmakokinetic Course 2009) Richard E. Carson gives the following hints on using weights:
▪Uniform weights (ordinary least squares fitting): Even if the data does not have uniform variance the estimates should be unbiased, but the parameter standard errors will be higher than they could be.
▪Wrong weights: The greater the error in the weights, the larger the loss of precision in the parameter estimates (more important for 11C than 18F).